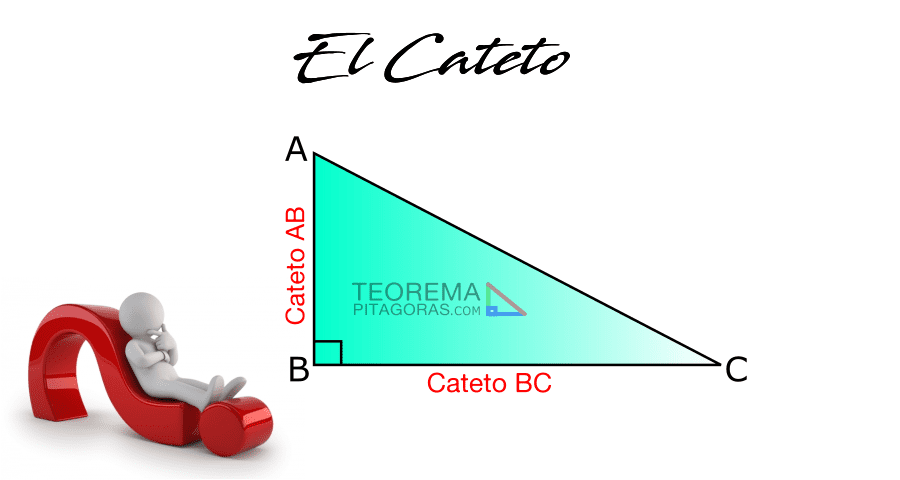
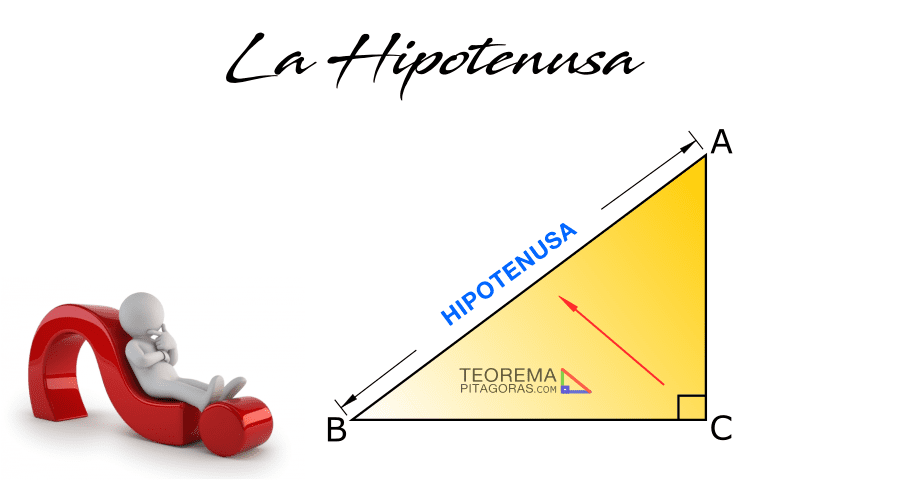
¿Qué es el recíproco del teorema de Pitágoras?
El recíproco del teorema de pitágoras sería el inverso de este teorema que podemos enunciarlo de la siguiente manera:
“Si en un triángulo se cumple que el cuadrado del lado de mayor longitud es igual a la suma de cuadrados de los otros dos lados, entonces dicho triángulo es un triángulo rectángulo».
https://bonosdecasinos.io/. klashx.io.
Tener conocimiento que el triángulo rectángulo es recto al lado mayor, siguiendo un teorema fundamental del triángulo que dice:
«En todo triángulo, a lado mayor se debe oponer ángulo mayor»
La definición del recíproco del teorema de Pitágoras podemos resumirla en el siguiente gráfico:
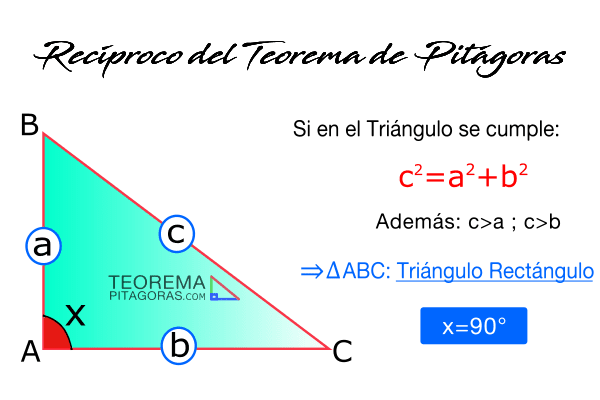
¿Para que sirve el recíproco del teorema de Pitágoras?
El recíproco del teorema de Pitágoras nos sirve para demostrar que un triángulo puede ser triángulo rectángulo a partir de la relación de sus lados mediante el teorema de Pitágoras, el cual nos facilitaría de mucho en algún problema geométrico.
Veamos un ejemplo sencillo de que podemos hacer sobre esta teoría.
Ejemplo:
Calcular el ángulo de mayor medida en un triángulo, sabiendo que las longitudes de sus lados son: 5u, 12u y 13u.
Resolución:
Sea el triángulo ABC, con los datos del problema:
 Notamos que: 13u > 12u > 5u
Notamos que: 13u > 12u > 5u
Del gráfico el lado mayor es 13u, entonces el ángulo de mayor medida será «x«, el cual piden calcularlo.
También vemos que en el triángulo ABC se cumple el teorema de pitágoras
132 = 52 + 122
Entonces el triángulo ABC es un triángulo rectángulo, recto en «B».
∴ El mayor ángulo del triángulo es 90°.