Teorema de Pitágoras

Web especializada en temas del teorema más famoso de la historia.

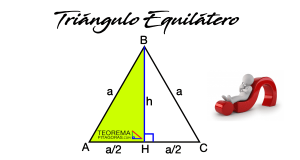
Triángulo Equilátero

Triángulo Equilátero: Definición y Fórmula para hallar la Altura

¿Qué es un Triángulo Equilátero? Un triángulo equilátero es aquel tipo de triángulo que tiene los …
Leer Más
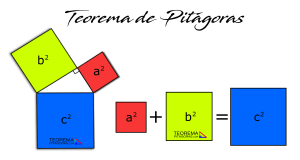
teorema de Pitágoras

Teorema de Pitágoras: Definición, Fórmulas y Ejemplos

¿Qué es el teorema de Pitágoras? El Teorema de Pitágoras relaciona los tres lados de un …
Leer Más
Teorema de Pitágoras Ejercicios

Teorema de Pitágoras: Ejercicios Resueltos paso a paso

En esta sección te enseñaremos cómo se resuelven los problemas del teorema de Pitágoras paso a …
Leer Más