Teorema de Pitágoras: Ejercicios Aplicando Trazos Auxiliares

Presentamos una colección de Problemas Resueltos de teorema de Pitágoras, aplicando trazos auxiliares. Estos problemas geométricos pueden clasificarse dentro de un nivel medio a difícil por lo que se requiere de un sólido conocimiento en Geometría para resolverlos.

Si Usted es un lector que tiene base teórica-práctica y desea pasar a otro nivel, entonces está en el lugar correcto.

Habrá podido apreciar que resolver problemas aplicativos al teorema de Pitágoras es fácil, lo complicado con los problemas que presentamos en esta oportunidad es buscar el triángulo rectángulo idóneo para relacionar los datos y lo que se está pidiendo.

Estamos seguros que los Problemas del Teorema de Pitágoras serán de su agrado, no olvide comentar de ser necesario o compartirlo para que pueda llegar a más personas y promover la educación libre.

El Teorema de Pitágoras

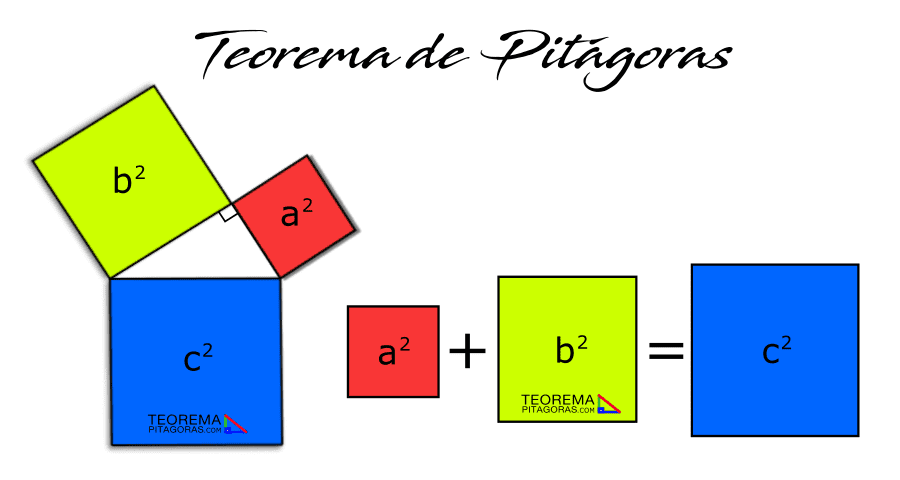
«En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de cuadrados de los catetos».

Gráficamente tenemos:

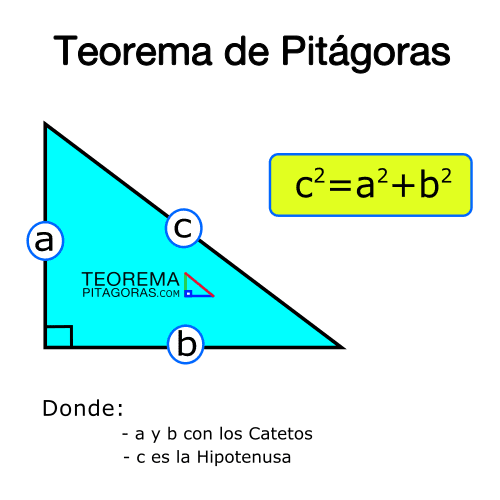
Teorema de Pitágoras Ejercicios

Ejercicio 01

Calcular el radio de la circunferencia tangente a los lados AB y BC del cuadrado ABCD mostrado. Si divide a los otros dos lados, en dos segmentos que miden 2m y 23m tal como se muestra en la figura:

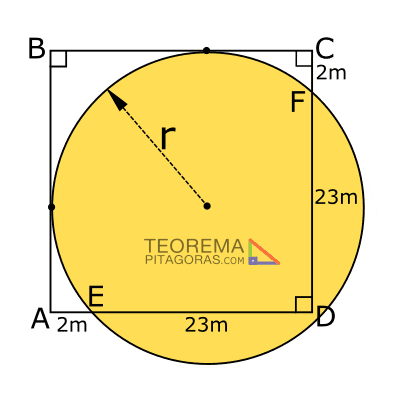
Resolución:

El problema nos pide calcular el radio «r».

Realizaremos unos trazos auxiliares con la finalidad de buscar el triángulo rectángulo donde aplicar el teorema de Pitágoras. Vea la figura:

Se ha realizado el trazo OF y la perpendicular OP al lado CD del cuadrado; formándose así el triángulo rectángulo OPF (sombreado).

ΔOPF:Luego de completar los lados y aprovechando el radio tenemos todos los lados del triangulo rectángulo en función de «r».

Aplicamos el teorema de Pitágoras.

r²= (25 – R)²+ (R – 2)²

Desarrollando la ecuación de segundo grado, tenemos:

∴ r =17m

Ejercicio 02

Halle la longitud de la hipotenusa de un triángulo rectángulo si las distancias del incentro de dicho triángulo a los extremos de la hipotenusa son 1u y √2u.

Resolución:

Graficando el problema según el enunciado, tenemos:

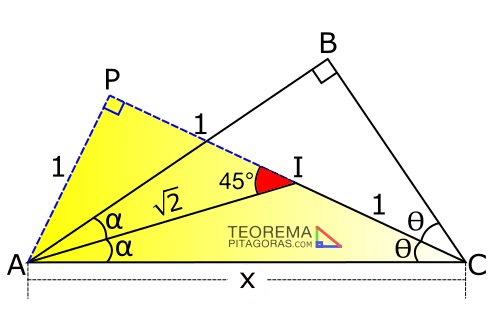
Observamos lo siguiente:

• Nos piden el valor de «x»
• «I»: Incentro del triángulo rectángulo ABC, por lo que el ángulo exterior en el vértice «I» del triángulo AIC es 45°, por propiedad.

Prolongamos CI hasta «P» para aprovechar el ángulo de 45° y formar el triángulo rectángulo notable API, por lo que:

AP = PI = 1u

Luego en el ΔAPC:Aplicación del teorema de Pitágoras.

x²= 1²+ 2²

Desarrollando tenemos:

∴ x =√5u

Ejercicio 03

Las distancia de dos puntos A y B a un mismo plano son 16u y 26u respectivamente. Si AB = 26u, calcule la proyección del segmento AB sobre dicho plano.

Resolución:

Realizamos la gráfica del ejercicio:

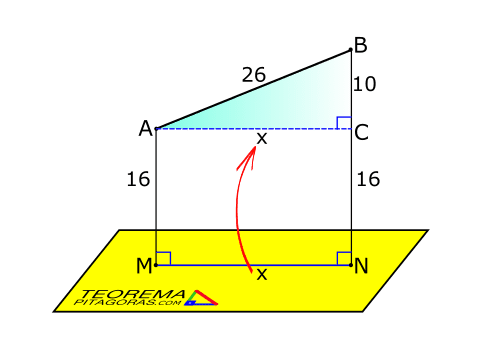El problema trata de un segmento de recta que se proyecta en un plano tal como se muestra en la figura. Teoría de Geometría del espacio.

Luego,«MN = x»será la proyección del segmento AB sobre el plano (amarillo), que es lo que nos piden. Realizando el trazo auxiliar AC perpendicular a BN generamos el triángulo rectángulo ABC.

⇒ AC = MN = x ∧ MA = NC = 16u

En el ΔABC:Aplicamos el teorema de Pitágoras.

x²= 26²– 10²

Desarrollando tenemos:

∴ x =24u

Ejercicio 04

Se tienen los cuadrados ABCD y ABEF, contenidos en planos perpendiculares, además AB = 2u. Calcular la distancia entre el centro del cuadrado ABEF y el punto medio del lado AD.

Resolución:

Realizamos el bosquejo del gráfico que señala el problema, tenemos:

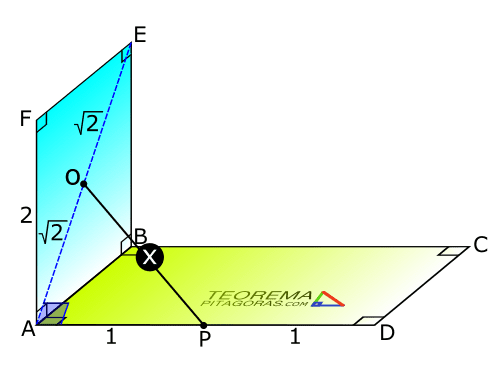
Se tiene:

• «O»: centro del cuadrado ABEF
• «P» Punto medio del lado AD.

Nos piden «OP = x»

Este problema también es de Geometría del espacio, donde realizaremos primero el trazo EA, el cual es la diagonal del cuadrado, por lo queOA = √2u

Luego en el puntoAse cumple el«teorema de las tres perpendiculares»; en consecuencia, se forma el triángulo rectángulo OAP, recto en «A».

Finalmente en el ΔOAP se aplica el teorema de Pitágoras:

x²= (√2)²+ 1²

∴ x =√3u

Ejercicio 05

En la figura mostrada se pide calcular MN, siendo M y N puntos medios de AM y PQ respectivamente. Además: a² + b² = 16u²

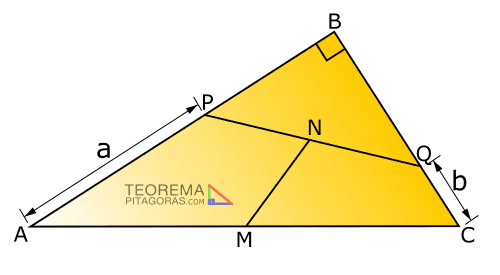
Resolución:

Sea:

MN = x

En este ejercicio se realizará un trazo auxiliar muy importante; pero, necesario para la resolución del problema. Se Traza AQ tal como se muestra en la siguiente figura:

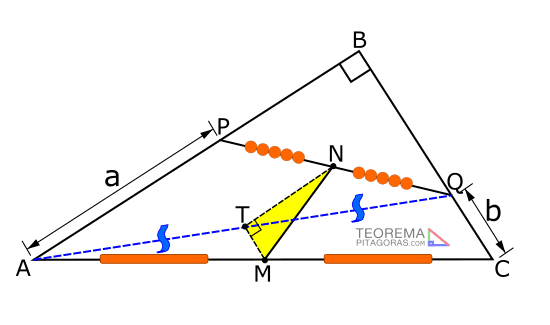
El Trazo AQ se realizó para aprovechar los puntos medios «M» y «N».¿Cómo?Así:

Se ubica el punto medio de AQ: «T»; entonces:

ΔAQP:TN es base o línea media de AP.

⇒ TN // AP; también:TN = a/2

ΔAQC:TM es base o línea media de QC.

⇒ TM // QC; también:TM = b/2

Observamos además que se ha formado el triángulo rectángulo MTN, el ángulo recto (90°) en «T» se da por las paralelas.

En el ΔMTN:

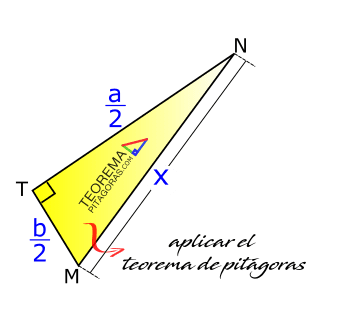
Aplicación del teorema de Pitágoras:

x²= (a/2)²+ (b/2)²

Desarrollando y reemplazando: a²+ b²= 16u²

∴ x =2m