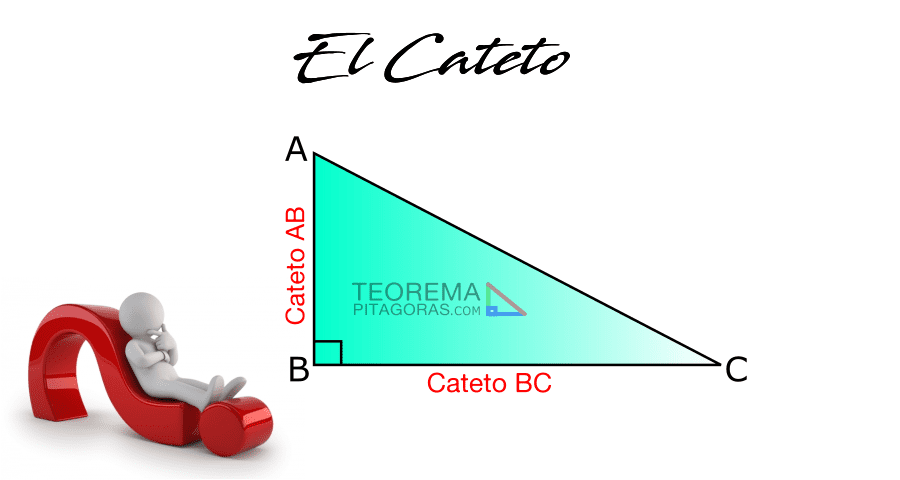
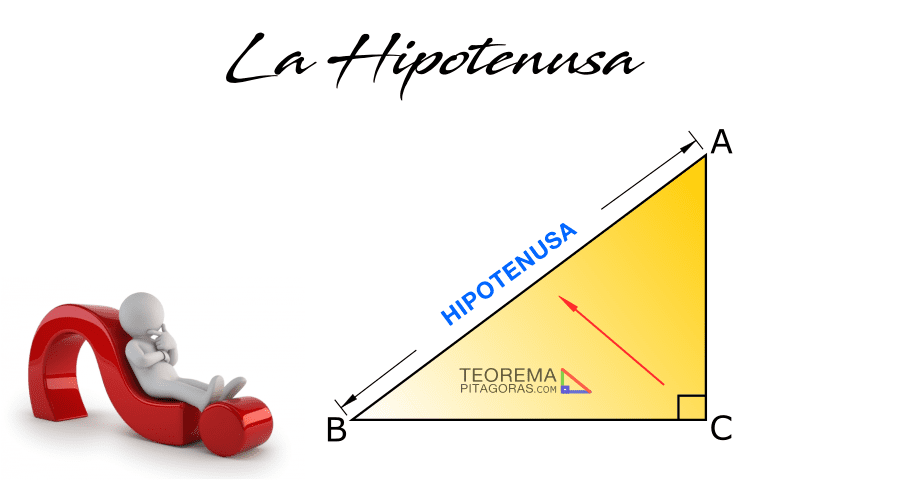
El teorema de Pitágoras ha sido y es actualmente importante en nuestras vidas por muchas razones. Por ejemplo, en la época antigua la navegación se llevaba a cabo gracias a cálculos en desuso: mirando las estrellas y siguiendo la línea de la costa.
“En todo triángulo rectángulo el cuadrado de la longitud de la hipotenusa es igual a la suma de cuadrados de las longitudes de los catetos”.
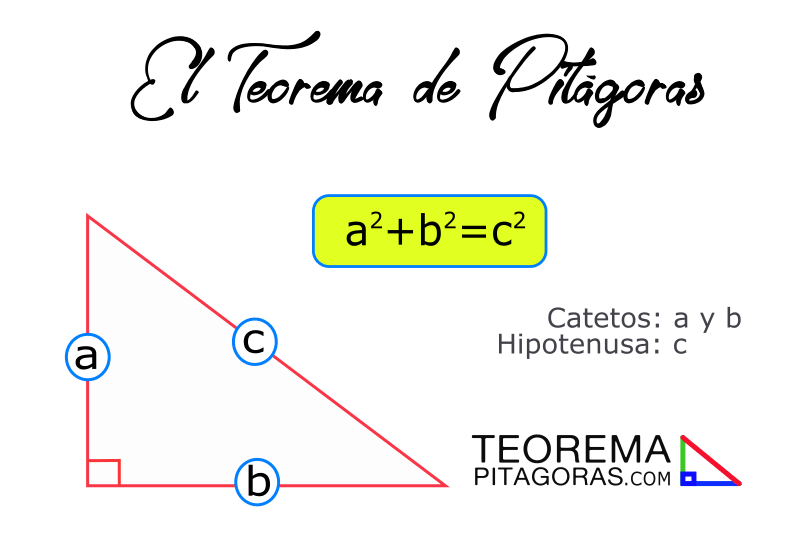
El teorema de Pitágoras cambió todo eso. Puso a la humanidad en la senda para la comprensión actual de la geografía de nuestro planeta y su lugar en el Sistema Solar.
Fue un primer paso vital hacia las técnicas geométricas necesarias para la cartografía, la navegación y la topografía. También proporcionó una vital relación entre la geometría, trigonometría y el álgebra.
El teorema de Pitágoras abrió por completo nuevas direcciones para la exploración humana, tanto metafóricamente como literalmente. Reveló la forma de nuestro mundo y su lugar en el universo.
Muchos de los triángulos que nos encontramos en la vida real no son rectángulos, de manera que las aplicaciones directas de la ecuación podrían parecer limitadas. Sin embargo, cualquier triángulo puede dividirse en dos triángulos rectángulos, y cualquier forma poligonal se puede dividir en triángulos.
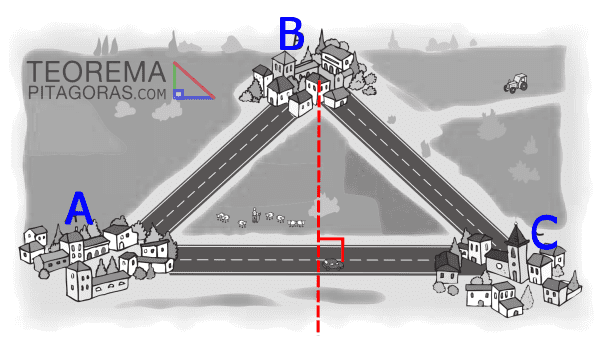
Así que los triángulos rectángulos son la clave, prueban que hay una relación útil entre la forma de un triángulo y la longitud de sus lados. La materia que se desarrolló a partir de esta visión es la trigonometría, que significa «medición de triángulos».
El teorema de Pitágoras fue también fundamental para la invención de la geometría analítica. Este es un modo de representar figuras geométricas en términos numéricos, usando un sistema de rectas conocidas como ejes, que se etiquetan con números.
La versión más popular es conocida como coordenadas cartesianas en el plano, en honor al matemático y filósofo francés René Descartes, que fue uno de los grandes pioneros en esta área, aunque no el primero.
Entonces, el teorema de Pitágoras es importante por sí solo, pero ejerce incluso más influencia a través de sus generalizaciones. La prueba del teorema de Pitágoras en los Elementos de Euclides coloca al teorema como pilar de la geometría.
Es una progresión de los eventos sorprendente. Primero surgió el teorema de Pitágoras hace alrededor de 3.500 años para medir la tierra de los campesinos. Su extensión a triángulos no rectángulos y a triángulos en la esfera nos permitió hacer mapas de nuestros continentes y medir nuestro planeta.
Y una egregia generalización nos permitió medir la forma del universo. Las grandes ideas a veces tienen comienzos humildes.